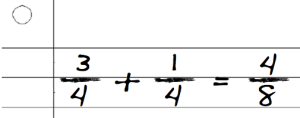Fractions were one of the trickiest topics for my students to learn. Prior to fractions, numbers made sense: they were whole, they increased in value as they got bigger, and they usually became larger when multiplied and smaller when divided.

With fractions, numbers were suddenly stacked on top of one another! Confusing words like “simplify” and “common factor” had to be memorized! When the numbers grew larger (1/4, 1/5, 1/6) their value decreased! In fact, they weren’t even called “numbers” anymore, but “numerators” and “denominators!”

It’s no wonder that fractions left my students scratching their heads.

But fractions aren’t only difficult for students with learning disabilities. On the NAEP (National Assessment of Educational Progress), half of all 8th graders couldn’t correctly order 3 fractions from least to greatest. So why are fractions so tricky for our students?

Here are some common mistakes my students have made and why they made them:

Students view the numerator and denominator as separate whole numbers instead of a single amount. They know that 7 is larger than 4, so naturally 2/7 must be larger than 2/4.

Students treat the numerator and denominator as whole numbers. Here they apply the properties of whole numbers to fractions: just as you would add 3+1=4 and 4+4=8, students apply their knowledge of addition to each separate part of the fraction.

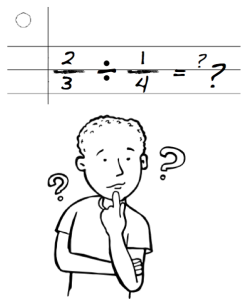Students struggle with multiplying and dividing fractions because the operations don’t result in the answer they expect. With whole numbers, students learned that division results in smaller numbers, and multiplication results in larger numbers.

However, the opposite is typically true for fractions. Division yields a larger quotient while multiplication yields a smaller product.

While students are often taught the procedural steps for multiplying and dividing fractions, they do so without understanding the underlying concept, leading to confusion in the later grades.

Students may have difficulty simplifying fractions because of a shaky understanding of division.

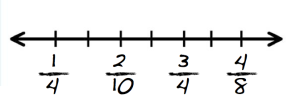Students often order fractions incorrectly and cannot place them on a number line. They cannot easily count fractions the way they count whole numbers (1,2,3,4…). Instead, there are infinite number of fractions between each fraction-- a fact that even college students have difficulty grasping.

Students overgeneralize rules for computing fractions. Once they learn that to keep the denominator the same when adding and subtracting fractions, they do the same when multiplying and dividing fractions.

Now that we know common mistakes students make with fractions and the underlying misunderstandings, what can we do about it? Our next blog post will explore simple instructional techniques teachers and parents can use to build their kids’ confidence with fractions.