I’ve always been slow. In high school, I ran cross country track because I wasn’t a sprinter. 

Same thing when it came to schoolwork. I was never the first to finish. I hated timed tests, like finishing as many multiplication and division problems as you can in one minute.

Even in grad school, I was always one of the last students left in the classroom, finishing my exam when everyone else was done.

Slow, but steady. I may not have been a sprinter, but I always finished my race. I may have been among the last to finish exams and hated timed tests, but I did well in school.

Too often, we overemphasize speed and underemphasize understanding and fluency in the math classroom. Learning math facts can be especially tricky for students with disabilities, who might have difficulty memorizing facts and trouble seeing relationships between related facts.

Remember those timed fluency drills your 3rd-grade teacher assigned? Turns out those drills aren't great at building true fact fluency!

Today I want to share what it really means to acquire “fact fluency.” Keep reading to find out why speed isn’t important and why flexible thinking is at the core of fluency.

What it takes to be “good at math”

If you took a poll and asked people what it means to be good at math, what do you think they’d say? I’d be interested to know what the students in your classroom would say, too!

I’d venture a guess that most people think being good at math has something to do with speed- how quickly you can calculate the tip at a restaurant, or mentally calculate 43 x 7.

And there’s certainly math skills involved in both those tasks. But being good at math is about so much more than how quickly you can solve problems. In fact, I think math aptitude has nothing to do with speed.

[Disclaimer: The link below is an affiliate link, which means I may get paid a commission if you purchase through that link, which comes at no cost to you.]

Adding it Up: Helping Children Learn Math conceptualizes math proficiency as having 5 related strands:

1. Conceptual understanding- understanding of math concepts, operations, and relationships
2. Procedural fluency- skill in carrying out procedures flexibly, accurately, efficiently, and appropriately
3. Strategic competence- ability to formulate, represent, and solve math problems
4. Adaptive reasoning- ability to think logically and reflect upon, explain, and justify one’s thinking
5. Productive disposition- habitual tendency to view math as practical, useful, and valuable, together with a belief in hard work and one’s own capabilities

Number and operations take up a large chunk of the math curriculum and we spend a good deal of time building our students' procedural fluency. Research shows that students with math disabilities demonstrate weaker math fact knowledge than their non-disabled peers, so fact fluency is certainly a skill we want to strengthen in our students. So what is fluency?

Myth #1: Faster is better: Math fact fluency is about speed

Notice how speed isn’t listed anywhere among those 5 strands necessary to become competent at math?

At its core, math is about finding relationships and patterns to solve problems, which involves the ability to think flexibly and strategically and communicate your thinking to others.

You don’t need to be a fast thinker in order to be a good thinker.

Myth #2: Procedural fluency doesn't build conceptual understanding

At first glance, the first two strands almost seem like opposites, don’t they?

We aim to build our students underlying conceptual understanding of math facts and procedures. For example, we want them to understand that 5 x 7 is 5 groups of 7. But we also aim to build their fluency with math facts and automatically know that 5 x 7 = 35.

So we have deep conceptual knowledge on the one hand and automaticity on the other hand.

Can we teach in such a way that we develop BOTH conceptual understanding and procedural fluency? I think you know the answer- a resounding YES!

In order to understand how conceptual understanding and procedural understanding are not opposites, but actually complementary and can be integrated into instruction, we need to take a closer look at fluency.

What is procedural fluency?

Procedural fluency, which we’ll also call fact fluency, is “skill in carrying out (computational) procedures flexibly, accurately, efficiently, and appropriately.” Let’s unpack each of these characteristics, using multiplication as an example:

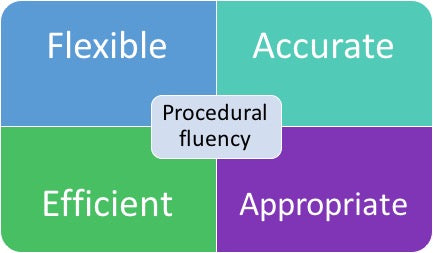
To flexibly know the multiplication facts, your students should know that 5 groups of 7 produce the same amount as 7 groups of 5. They should be able to apply multiple strategies for multiplying whole numbers, such as using related facts, drawing a picture or using manipulatives, and using skip counting or repeated addition.

To accurately know the multiplication facts, students should get the right answer most of the time (I like to leave a little wiggle room, we all get things wrong sometimes :)

To efficiently know the number facts, it should be an effortless process that doesn’t tax students’ working memories. They should also be able to choose the best, more efficient process to arrive at a solution. Drawing an array of 5 rows and 8 columns of circles then adding up all the circles is far more time consuming than using the related fact 5 x 7 = 35 to answer 5 x 8.

To appropriately know the number facts, students should know when to use procedure and how to apply it to novel situations. For example, you use 3 tablespoons of sugar to bake 6 cupcakes. How many tablespoons of sugar do you need to double the recipe and make 12 cupcakes? To figure out this problem, students need to know which operation is appropriate to use.

Myth #3: You need to memorize the math facts to become fluent

Math fact fluency is not the same as memorization.

Let’s imagine you’re working with Ricardo in your class. You start posing multiplication problems to Ricardo: 3 x 6, 2 x 4, 8 x 5. Ricardo rattles off each answer immediately: 18, 8, 40.

Is Ricardo demonstrating multiplication fluency? Not necessarily! A lot of people equate fluency with memorization, but they’re actually two different things.

Memorization does not indicate understanding or fluency. You can have a strong memory and commit all the times tables to heart.

Ivan Pavlov, a behavioral psychologist, would boil it down to stimulus and response: You’re exposed to the stimulus enough times (5 x 7) and rewarded for the correct response (35). Eventually, you associate the two.

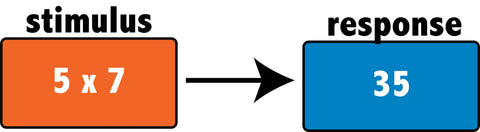
So, what’s the problem with rote memorization?

If we’ve just memorized all the multiplication facts, we’re probably accurate and efficient. But remember, those are only half the characteristics of fluency. Rote memorization alone doesn’t lead to flexible thinking and appropriate use of the procedure.

Rote practice of facts, using common tools like flash cards or timed worksheets, also make a few incorrect assumptions:

• Students are blank slates with no prior knowledge. They cannot learn computational concepts, such as multiplication, based on their previous math experiences.

• Students cannot reason or think strategically to solve problems. Instead, they learn best when repeatedly practicing the facts until they are committed to memory.

• Student’s don’t need to understand the underlying concepts, like the meaning of multiplication. They just need to be able to answer fact problems quickly and correctly.

Rote memorization is also harmful because it isn’t related to any meaningful or purposeful experiences. It’s decontextualized from children’s everyday lives, so they don’t have the joy of learning how computational thinking helps them in common situations.

Rote memorization is also dull and repetitive. I’m sure many of you have memories of those timed drills, which can be anxiety-inducing, or stacks and stacks of flashcards. These are probably not happy memories.*

Math can be exciting, interesting, and relevant- when taught correctly. Many struggling learners develop an aversion towards math and teaching math as a series of unrelated, meaningless facts that need to be memorized won’t create motivated, interested learners.

It also doesn't create successful students. Students who relied on memorizing math facts performed the lowest on the PISA test.

Finally, kids with disabilities often already have weak memories. They have trouble keeping information active in their working memories and retrieving facts from their long-term memories. If the only way they’ve been taught how to multiply is through memorization, they’re already set up for failure.

You're saying I should NEVER use fact fluency drills?

Not exactly- I'm saying that computation instruction should be problem-based and focus on applying strategies and reasoning to solve problems.

But after students have had a lot of experience solving problems by applying reasoning strategies and modeling them with manipulatives and drawings, they might still struggle with the automatic retrieval of facts. In this case, research shows that drill can be effective to help strengthen students' automatic recall of facts.

And there are other teaching strategies you can use to improve your students' fact fluency.

Why is it important for students to learn (and understand) the facts?

We do want students to recall math facts from memory accurately and efficiently. This helps them move onto learning more complex math concepts. The automaticity of knowing their math facts also frees up space in their minds for other kinds of thinking, such as applying multiplication facts to solve problems.

However, from memory is not the same as memorization. Students who have been given a lot of practice working with numbers and creating equal groups in varied contexts can eventually “know” that 3 x 7 = 21, without relying on rote memorization.     

Read more here about how to teach fact fluency so that students know their facts from memory.

Wrapping it up:

Think back to when you were in school. Remember those timed drills, worksheets with seemingly endless rows of math facts to solve? Or those flashcards your teacher held up as your classmates stood up, one at a time, to quickly answer?

Turns out you didn’t need to solve 40 problems in a minute or get anxious in front of your class to learn your math facts!*

*A note about those timed fact fluency tests: some of you might have loved the challenge of answering as many questions as you could in one minute. It's true that some of our students will enjoy timed tests while others will dread them. But regardless of how students feel about them, timed fluency drills don't build true fluency. They don't help students learn to use numbers flexibly, connect related facts, and know which operation is appropriate in a given situation. 

In this blog post, we learned:

• Math fact fluency ISN'T about answering math facts quickly or memorizing the facts.

• Math fact fluency IS about flexible, accurate, efficient, and appropriate thinking. 

• Becoming fluent with math facts can actually build conceptual understanding of number facts and how they're related!

[Disclaimer: The link below is an affiliate link, which means I may get paid a commission if you purchase through that link, which comes at no cost to you.]

Do you want to learn more about fact fluency?

One of my favorite resources, especially when thinking about my students with learning disabilities, is Achieving Fluency: Special Education and Mathematics by NCTM. 

Now that you're ready to boost your students' math fact knowledge, learn some ways you can develop true fluency in the classroom here. 

In the meantime, go ahead and ask your students what they think it means to be good at math. Share their answers in the comments below, I'm curious what they'll say!