Avoid the confusion: attack tricky math vocabulary head-on
SCROLL DOWN TO THE BOTTOM TO GET YOUR FREE COPY OF OUR MATH VOCABULARY TOOLKIT
We had the best of times practicing our times tables.
What an odd number those odd numbers are! And the even numbers are even stranger!
Don't be mean and not help me find the mean of all these numbers!
You can count on me to always count on from the larger number when I add in my head.
Is right angle the right answer? I'll write it in on the board.
Learning math words is hard! Your finger digit is different than a number digit. The kind of operations hospitals do is quite different than the kind of operations we do in math class.
(These sentences were really fun to come up with! Try to write a few yourself and leave them in the comments.)
There are concrete, actionable steps we can take to help our students learn math vocabulary words, as we've already seen.
Today, we'll take a closer look at some examples of the kinds of math vocabulary that trip up our students, especially those with learning disabilities and English Language Learners.
We'll talk about WHAT kinds of math words are tricky and HOW to help students overcome the confusion so they can communicate mathematically.
But before we get into it, a quick caveat: The following strategies will help your students learn what math words SOUND like and their DEFINITIONS, which will help them communicate their math thinking. But the strategies aren't intended to build CONCEPTUAL UNDERSTANDING.
For example, we'll learn a strategy below to help differentiate between the similar sounding ten and tenth, but the strategy won't help students know that a tenth is created when we divide one whole into ten equal parts.
But using both explicit language instruction AND teaching the concepts will help students connect the meanings with the right math words.
Ok, onto the tricky math words...
Tricky words #1: The teen numbers
Come on and count with me.
We’ve got 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. So far so good.
Since we know our number system is a base-10 system, we know we start again at 10. Here is where things start to get shaky.
10 + 1 = eleven
10 + 2 = twelve
10 + 3 = thirteen
10 + 4 = fourteen
10 + 5 = fifteen, and so on.
Eleven and twelve don’t seem to follow any set pattern, unlike the numbers 13 through 19. They’re an irregularity to the pattern.
But even the teen numbers are tricky. We say thirteen, for example. Why not threeteen?
Fourteen starts to make more sense. “Four” + “teen.”
But, like all the teen numbers, we say the “four” part first, but we write the digits in the opposite order- the 1 is first, followed by the 4.

This is one reason why children sometimes reverse the digits and write 41 instead of 14, and 51 instead of 15, and so on.
To add even more confusion to our number names, let’s make our way to the decades. Fifty sounds an awful lot like fifteen, doesn’t it? And sixty sounds like sixteen. And seventy sounds like seventeen. You get the idea.
If you think the decades sound a lot like the teen numbers, image a child who has expressive or receptive language delays. They have a difficult time distinguishing the sounds in words so the “-ty” in “fifty” doesn’t sound much different than the “-teen” in “fifteen.”
Our number words aren't making it easy for our students, are they? But there are a few things we can do to help clear up the confusion.
How to teach the language of the teen numbers
1) Explicitly teach the number words and explain that some numbers break the pattern. Don’t assume that students will learn the correct way to read and write the teen numbers on their own through repetition or experience. Make it a point to teach the numbers.
We spend a lot of time teaching our students to look for patterns in math, like finding patterns in the 100s chart. But explain that 11 through 19 "are funny numbers that don’t follow the rule.”
Stretch out the sound of the ending of each word and use color coding to emphasize the ending.

You can also use color coding to show that we read most of the teen numbers backward, from right to left. I like to use green and red when I color code: green means start, red means stop.
2) Students should practice saying the number words when using concrete manipulatives, like base-10 blocks or bundles of popsicle sticks. Have students practice making numbers and reading them aloud with partners.
Here’s a simple activity:
- Create a set of cards with the teen numbers and decade numbers written on them.
- Each student draws a card and makes that number with base-10 blocks or stacks of popsicle sticks.
- The student reads the number aloud.


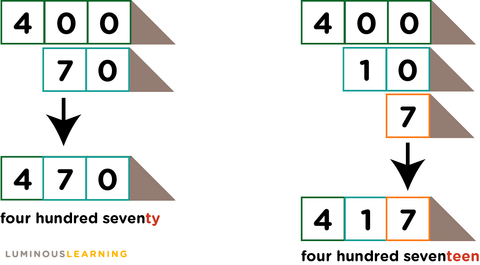
3) Use place value arrow cards to practice reading numbers. These are great tools to use when teaching the difference between ones and tens and hundreds.
But you can also use them to help students understand the difference between the teens and the decades: fourTEEN and forTY, fifTEEN and fifTY, etc.
Scroll down to the bottom to get a FREE copy of our place value arrow cards.
Tricky words #2: The everyday words
Children hear and use words in their everyday lives that take on different meanings in the math classroom. Imagine students' confusion when the teacher is talking about the faces of a shape and students are thinking about the face on their heads and wondering what their face has to do with that shape.

Us smart, competent adults naturally understand the multiple meanings of words. For example, you can carry your backpack and you can carry the digit in the ones column to the tens column when you regroup.
We easily understand and accept both definitions, but sometimes fail to realize that our students can’t shift gears as easily and apply different definitions in different situations.
Just look at some of these examples:

Scroll down to the bottom to get a FREE copy of our math homophones infographic.
We need to think carefully about the words we use to describe math ideas and define tricky words that have different meanings in everyday life.
How to teach everyday words with multiple meanings
Some of my favorite tools:
- The word wall and personal word banks
- Math journals
- Graphic organizers, like the Frayer Model

Learn more about how to use these in the math class here.
Scroll down to the bottom to get a FREE copy of our Frayer Model for math vocabulary.
Tricky words #3: The decimal number words
This one's similar to the -teen and -ty numbers.
Tenth sounds an awful lot like ten.
Hundredth sounds an awful lot like hundred.
Thousandth sounds an awful lot like thousand.
One more thing: the decimal point. We call that dot we use to separate whole numbers and decimals a "decimal point."
But when we read a decimal number, do we say: "eight decimal point three tenths?"
No, we say: "eight AND three tenths."

How to teach the decimal number words:
Two strategies I like to use to clear up the confusion with decimal words are:
1) Color coding. Make the -ths stand out on your anchor charts, posters, handouts, and Smartboard slides. Make the -ths bold and colorful.
Emphasize and stretch out the -ths sound when you read the word. Have fun with it and see which students can make the -ths sound the loudest or hold it the longest. They'll get a little spittle on their desks, but it's ok for math to get messy sometimes :)
2) Play "unscramble the numbers" game! Games always make math more fun, right? Here's what you do:
- Make cards with the number words (I like to have the actual numbers printed on the cards, for my students who have trouble reading.)
- Make cards that read: and, tenth, hundredth, thousandth (only make the cards for the place value you've already taught.)
- Students work in pairs. One student takes a few cards and unscrambles them to make an actual number. The other student writes the number, in symbols, on a whiteboard or paper. Then they switch.

Tricky words #4: The addition and subtraction words
Words we use when we add include: plus, add, and, altogether, join, sum, combine, both, in all, total, increase, more, how many.
Words we use when we subtract include: minus, subtract, difference, left over, take away, less than, decrease, reduce, remove.
Our students with disabilities like consistency and can have a hard time accepting new words that mean the same thing. Let's look at a few different ways we can read the following equation: "3 + 4"
- What is the sum of three plus four?
- What is 3 and 4 more?
- How much is 3 and 4, altogether?
- Combine 3 and 4.
Your student Jasmine learned that this + symbol is called "plus." But we only used the word plus in the first example. Jasmine needs to accept that there are many different ways to express adding.
Not only that, but some of the words that signal addition can ALSO signal subtraction, based on the context. Let's take "altogether," for example:
- The squirrel gathered 3 acorns on Monday and another 4 acorns on Tuesday. How many acorns did the squirrel gather altogether?
- The squirrel gathered 7 acorns altogether. If it gathered 3 acorns on Monday, how many acorns did it gather on Tuesday?
If Jasmine thinks that "altogether" always means to add, she'll automatically (and incorrectly) add 7 + 3 in the second word problem, instead of subtracting 7 - 3.
I'll step on my soapbox for a moment and stress that this is why we shouldn't teach cue words (aka clue words or key words) for solving math problems!
Stepping off my soapbox...
Another confusion? The symbols we use to add and subtract.
+ can mean add. But + can also mean positive, as in "It's +12° outside."
- can mean subtract. But - can also mean negative, as in, "It's -12° outside."
(either way, it's pretty cold out!)
How to translate the language of word problems:
Two strategies that can help students learn how to translate the words in a problem and choose whether or add or subtract (or multiply or divide, for that matter) are:
1) Act it out. Have students act out a word problem with a partner.
This helps them focus less on the individual words that won't necessarily help them understand the problem (e.g., "altogether") and instead help them focus on the overall meaning of the problem. Once they understand what's happening in the problem, they're better equipped to choose a method to solve it.
2) Draw it out. If acting isn't your thing or their thing, students can also draw a picture to show what's happening in the word problem. This achieves the same goal as above and helps students focus on the big picture or overall meaning.
3) Take out the numbers. Sometimes I find my students ignore the words completely, pick out the numbers, and perform a random operation on them. With no regard to whether the problem calls for addition or subtraction or multiplication or division.
So I slow it down and take the numbers out of the word problem. Can't add numbers when there aren't any, right?
Without the numbers to distract them, students are forced to focus on the meaning and explain what the problem is asking.
Wrapping it up:
In this post, we talked about 4 kinds of tricky math words:
- The teen numbers
- The everyday words
- The decimal words
- The addition and subtraction words
We also talked about ways to teach these tricky words so that they no longer confuse students.
As a reminder, these strategies are primarily meant to help students learn the LANGUAGE of math, not help them learn math CONCEPTS. Of course, we want to use a number of strategies together so that students learn both math vocabulary AND concepts.
If you want to learn more about vocabulary instruction, two of my favorite books are:
[Disclaimer: The links below are affiliate links, which means I may get paid a commission if you purchase through those links, which comes at no cost to you.]
- Building Academic Vocabulary: Teacher's Manual by Marzano and Pickering
- Bringing Words to Life: Robust Vocabulary Instruction by Beck, McKeown, and Lucan
(note that these books aren't specific for math vocabulary instruction, but you can apply the knowledge in the books to teaching math words)
Now your turn! Tell me what math words your students find confusing. How do you help them understand and use those words?

